Results

Results have been obtained by taking the minimum run time across five trials on an AMD EPYC 7702 2.0GHz processor. Randomized alogrithms were made deterministic by fixing their random seed. Performance evaluation is done as proposed by [Beiranvand2017].

Fixed-Time Performance Evaluation

For fixed-time performance evaluation we restrict run time (1, 10, 100s) and evaluate attained objective values, lower bound and, for datasets with ground truth available, accuracy. We also report the number of optimally solved instances per dataset. For this we consider solutions within a 0.1% range to known optimum as optimal. To show the detailed results for each dataset please follow the links below:

Fixed-Target Performance Evaluation

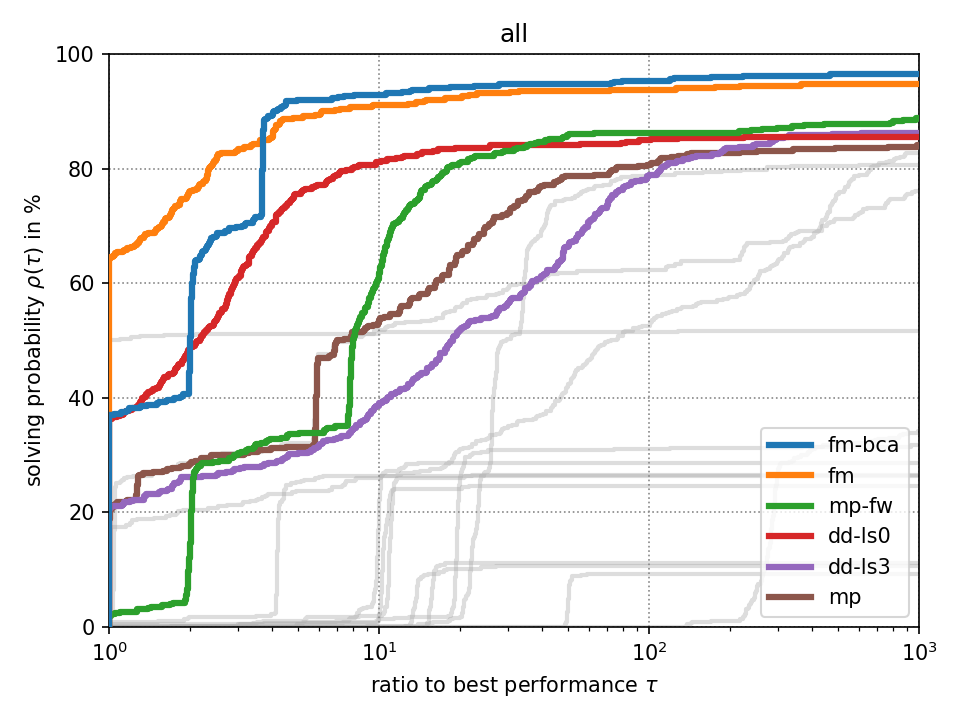
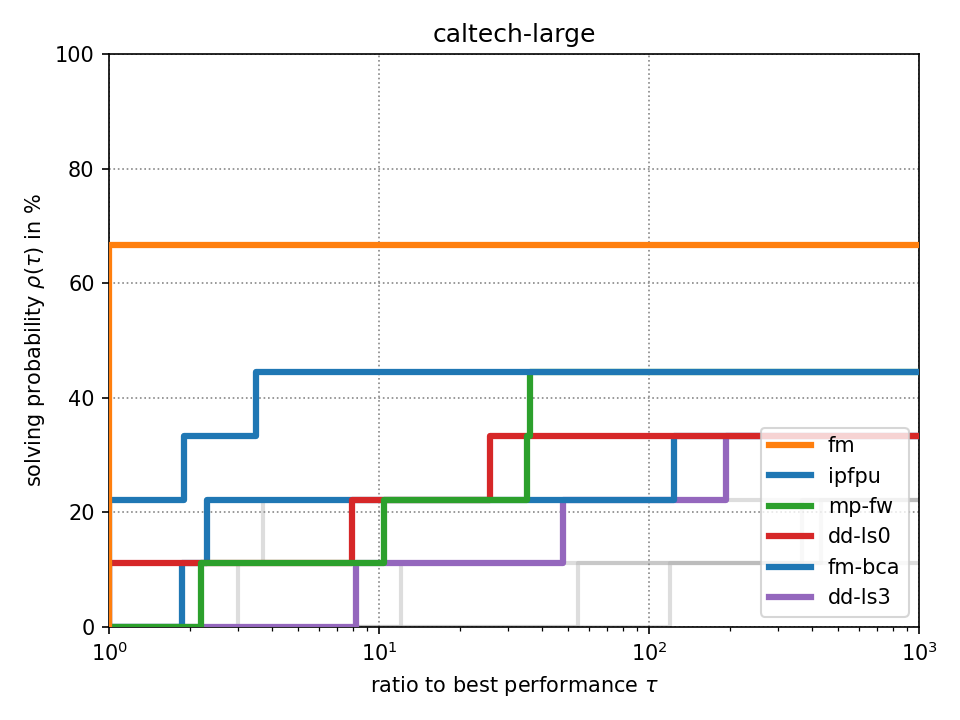
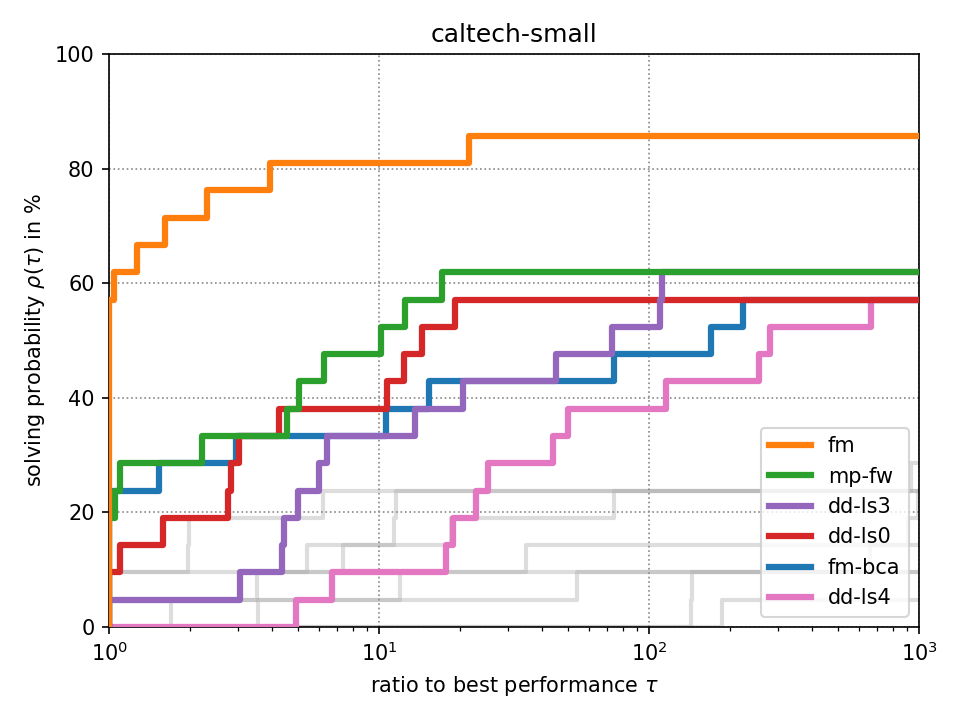
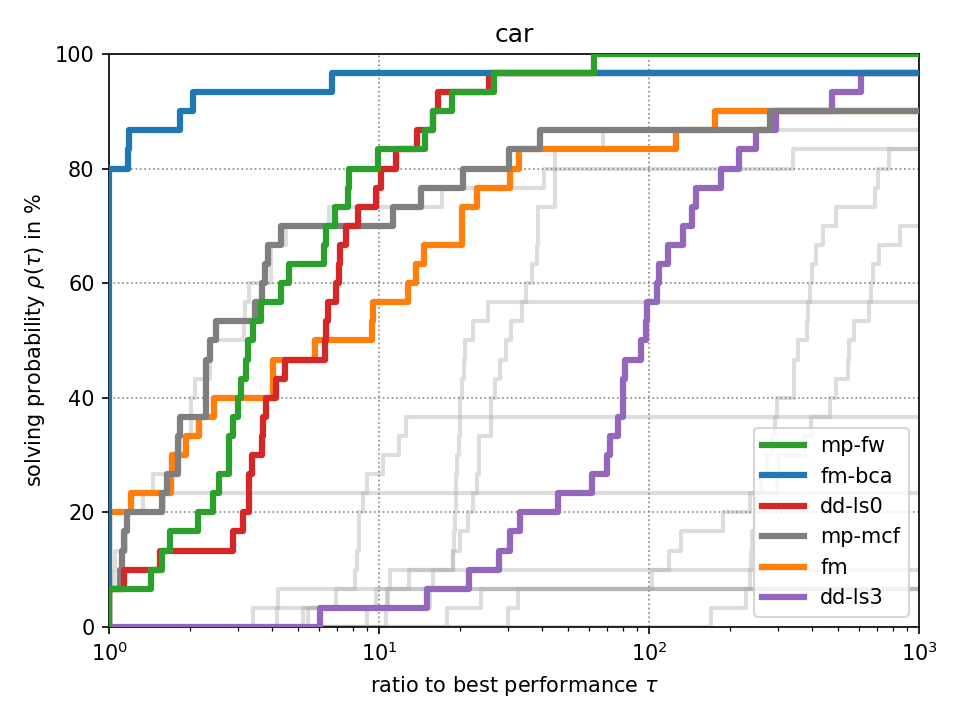
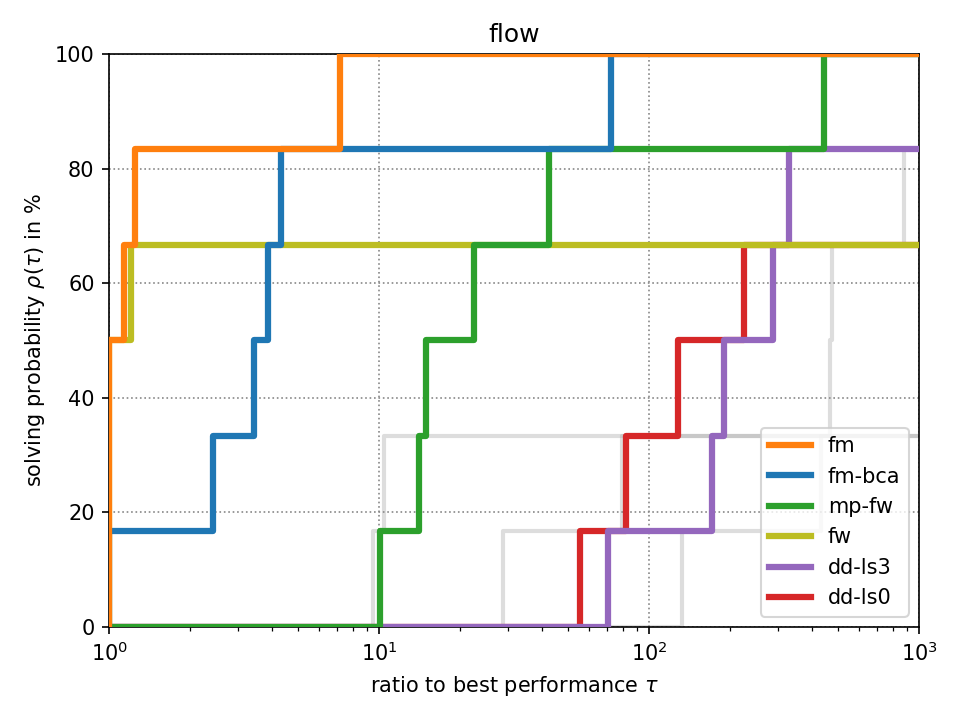
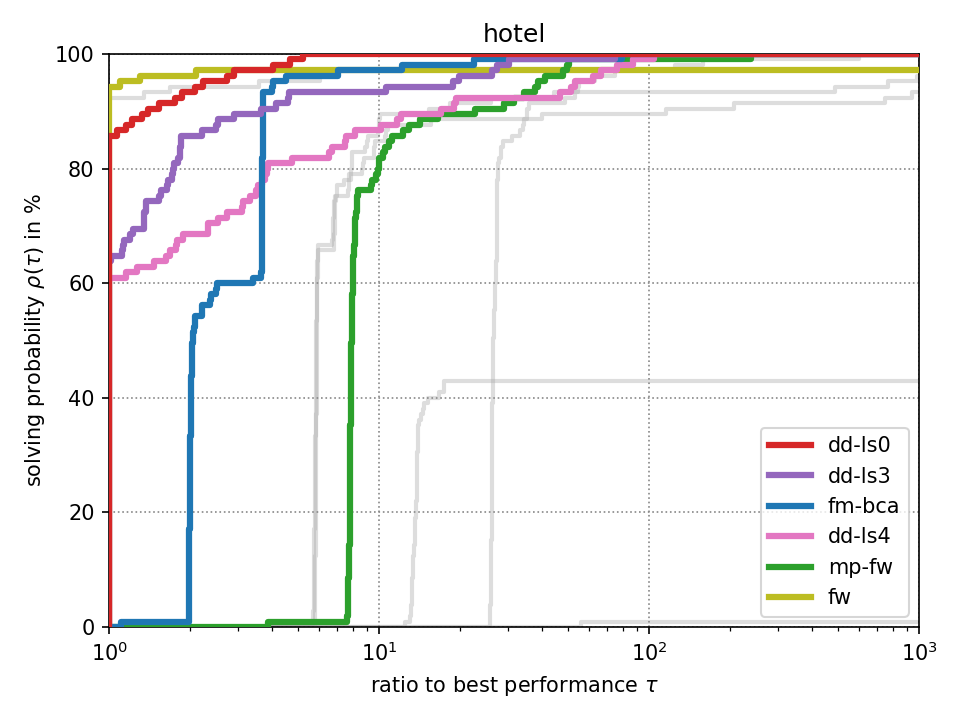
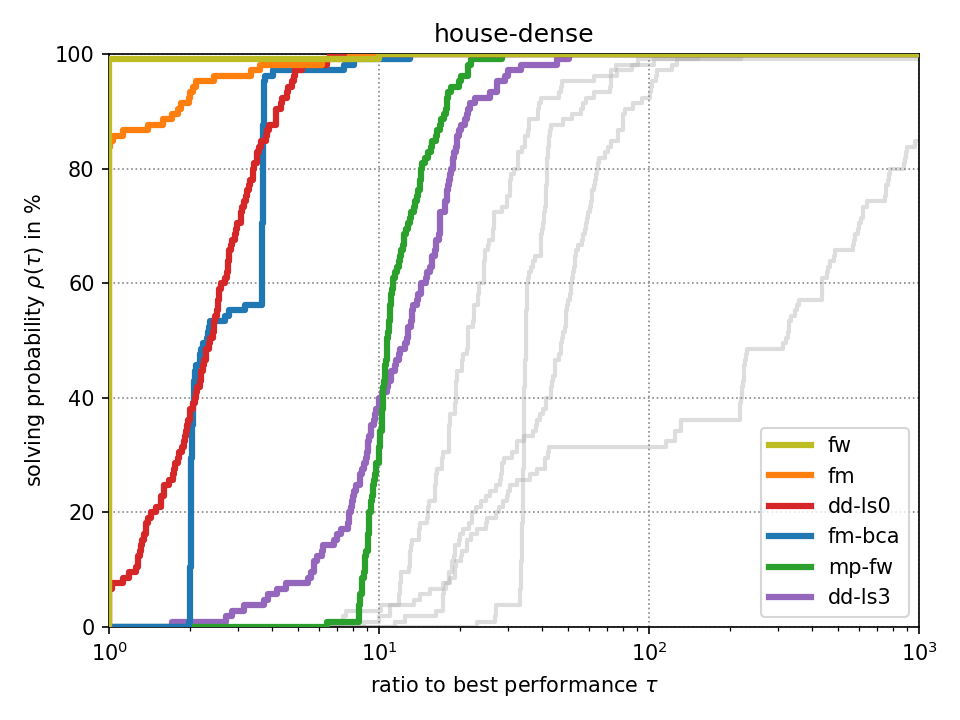
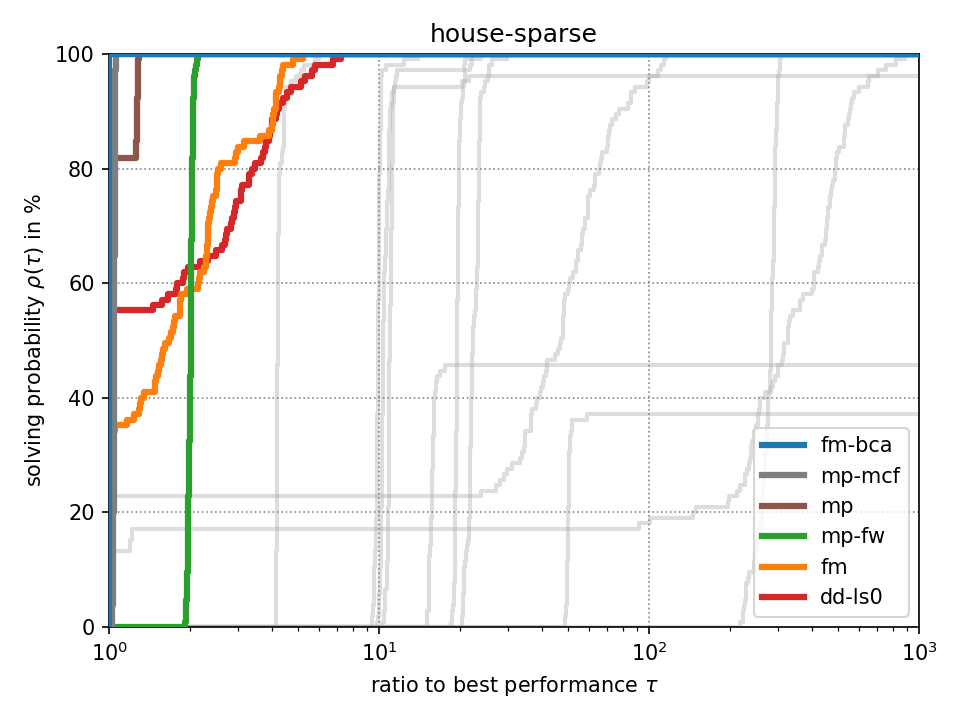
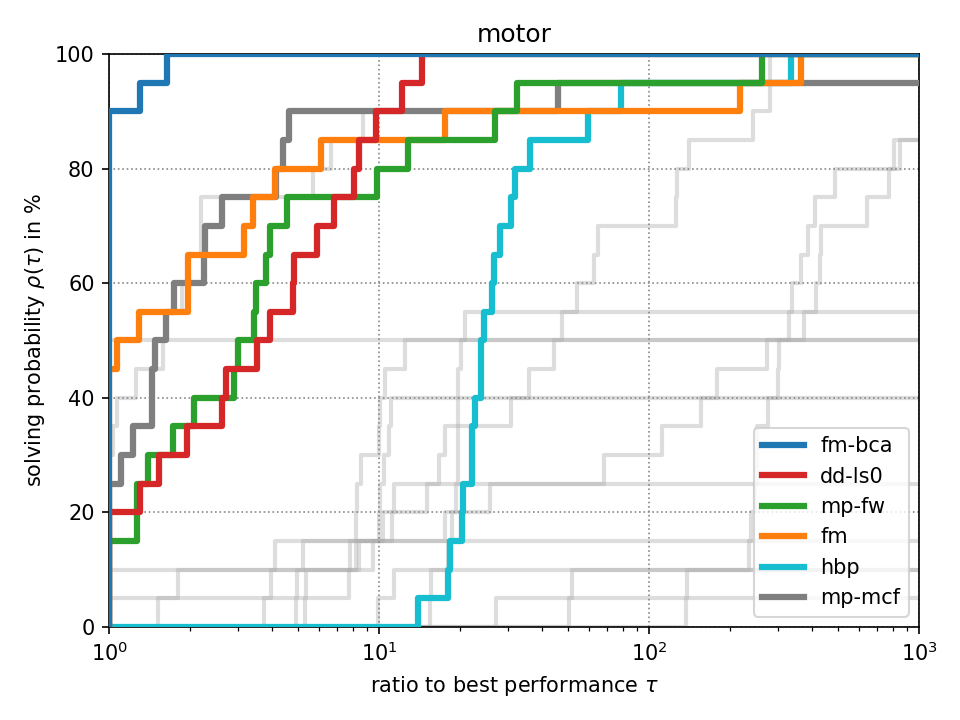
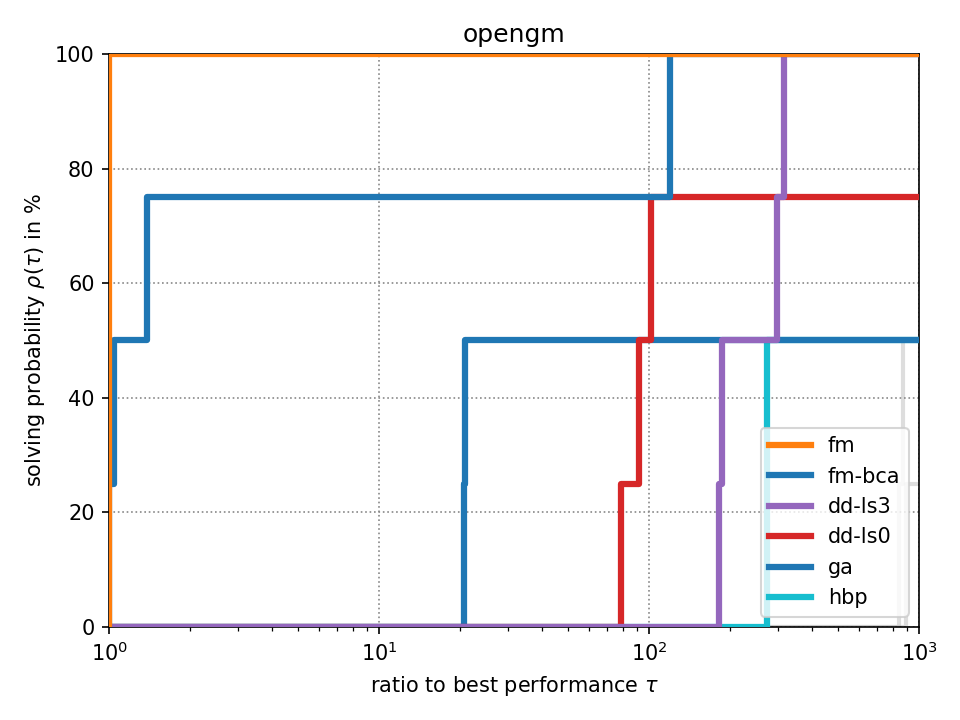
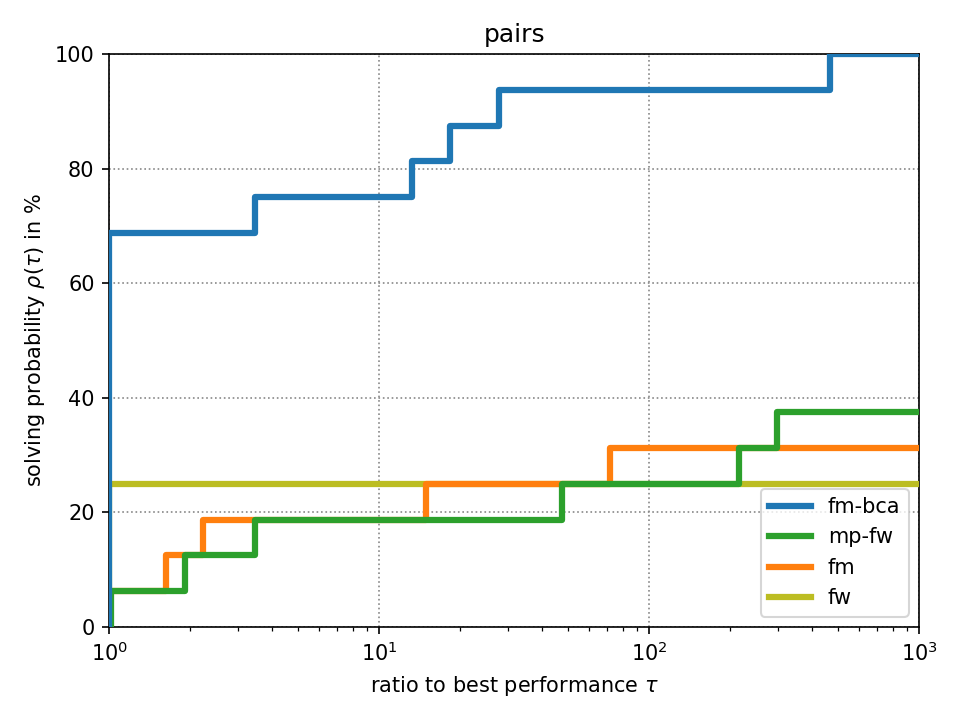
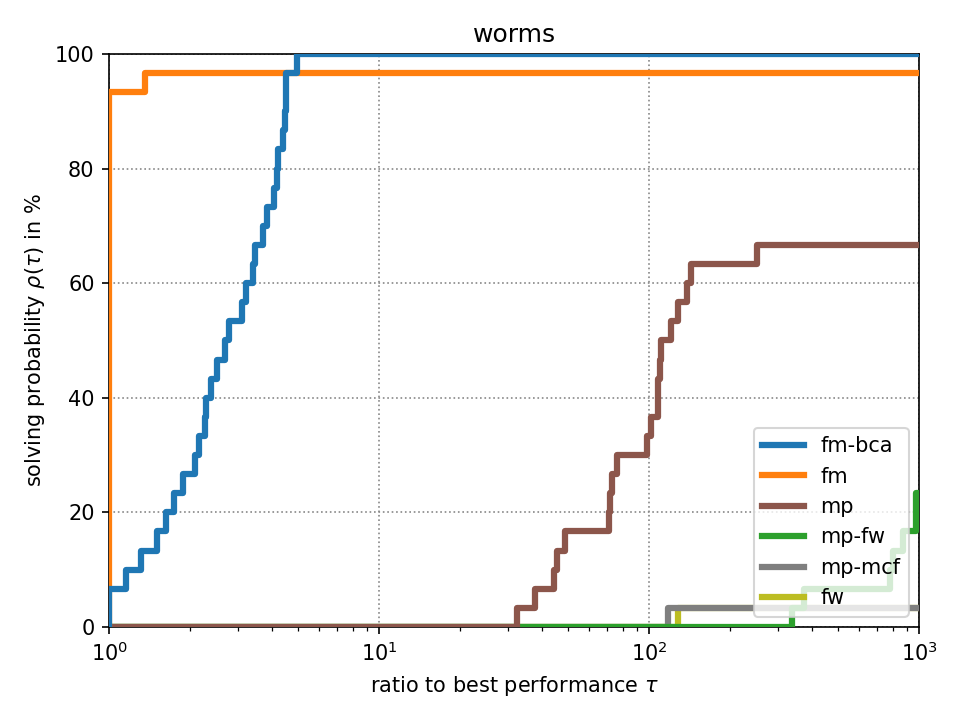
For fixed-target performance evaluation we measure the time \(t_s(p)\) until each solver \(s\) solves the problem \(p\) within an optimality tolerance of 0.1%. For instances with unknown optimum, we consider the best achieved objective value across all methods as optimum as it has been suggested in [Beiranvand2017]. The performance ratio to the best solver is computed by \(r_s(p) = \frac{t_s(p)}{\min \{ t_s(p) : \forall s \}}\). We create a performance profile [Dolan2002] by computing \(\rho_s(\tau) = \frac{1}{|P|} \cdot |\{ r_s(p) \leq \tau : \forall p \}|\) for each solver \(s\) where \(|P|\) denotes the total number of problem instances. Intuitively, \(\rho_s(\tau)\) is the probability of solver \(s\) being at most \(\tau\) times slower than the fastest solver.