Computation graph API#
The building blocks of the INN computation graph are the nodes in it.
They are provided through the FrEIA.framework.Node class.
The computation graph is constructed by constructing each node, given its
inputs (defining one direction of the INN as the ‘forward’ computation).
More specifically:
The
Node-subclassInputNoderepresents an input to the INN, and its constructor only takes the dimensions of the data (except the batch dimension). E.g. for a 32x32 RGB image:in1 = InputNode(3, 32, 32, name='Input 1')
The
nameargument can be omitted in principle, but it is recommended in general, as it appears e.g. in error messages.Each
Node(and derived classes) has propertiesnode.out0,node.out1, etc., depending on its number of outputs. Instead ofnode.out{i}, it is equivalent to use a tuple(node, i), which is useful if you e.g. want to loop over 10 outputs of a node.Each
Nodeis initialized given a list of its inputs as the first constructor argument, along with other arguments covered later (omitted as ‘...’ in the following, in particular defining what operation the node should represent). For Permutation in the example above, this would look like the this:perm = Node([in1.out0], ..., name='Permutation')
Or for Merge 2:
merge2 = Node([affine.out0, split2.out1], ..., name='Merge 2')
Conditions are passed as a list through the
conditionsargument:affine = Node([merge1.out0], ..., conditions=[cond], name='Affine Coupling')
The
Node-subclassOutputNodeis used for the outputs. The INN as a whole will return the result at this node.Conditions (as in the cINN paper) are represented by
ConditionNode, whose constructor is identical to theInputNode.Take note of several features for convenience (also see examples below): 1.) If a preceding node only has a single output, it is also equivalent to directly use
nodeinstead ofnode.out0in the constructor of following nodes. 2.) If a node only takes a sinlge input/condition, you can directly use only that input in the constructor instead of a list, i.e.node.out0instead of[node.out0].From the list of nodes, the INN is represented by the class
FrEIA.framework.GraphINN. The constructor takes a list of all the nodes in the INN (order irrelevant).The
GraphINNis a subclass oftorch.nn.Module, and can be used like any other torchModule. For the computation, the inputs are given as a list of torch tensors, or just a single torch tensor if there is only one input. To perform the inverse pass, therevargument has to be set toTrue(see examples).
Above, we only covered the construction of the computation graph itself, but so
far we have not shown how to define the operations represented by each node.
Therefore, we will take a closer look at the Node constructor and its
arguments:
Node(inputs, module_type, module_args, conditions=[], name=None)
The arguments of the Node constructor are the following:
inputs: A list of outputs of other nodes, that are used as inputs for this node (discussed above)module_type: This argument gives the class of operation to be performed by this node, for exampleGLOWCouplingBlockfor a coupling block following the GLOW-design. Many implemented classes can be found in the documentation under https://vll-hd.github.io/FrEIA/modules/index.htmlmodule_args: This argument is a dictionary. It provides arguments for themodule_type-constructor. For instance, a random invertible permutation (module_type=PermuteRandom) can accept the argumentseed, so we could usemodule_args={'seed': 111}. If no arguments are specified we must pass an empty dictionary{}.
Using these rules, we would construct the INN from the example
in the Basic concepts section:
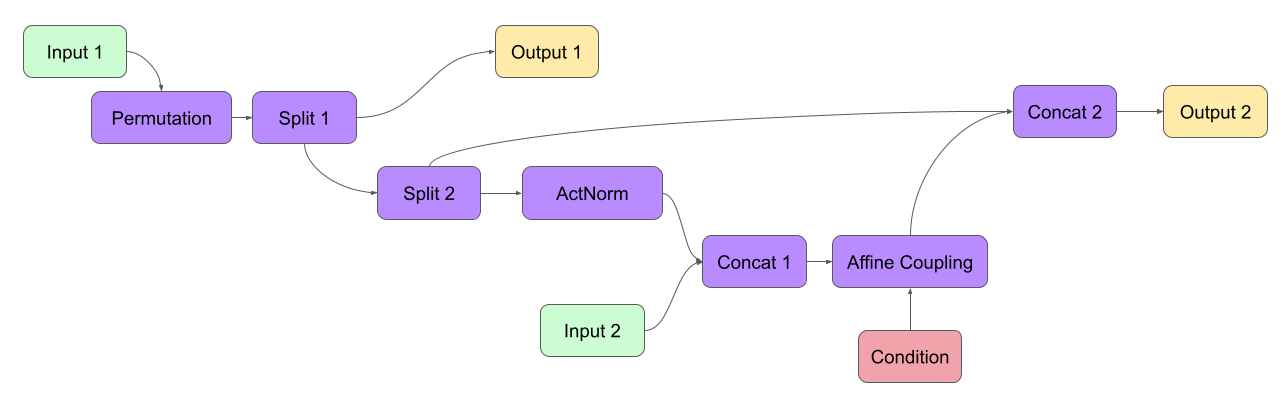
in1 = Ff.InputNode(100, name='Input 1') # 1D vector
in2 = Ff.InputNode(20, name='Input 2') # 1D vector
cond = Ff.ConditionNode(42, name='Condition')
def subnet(dims_in, dims_out):
return nn.Sequential(nn.Linear(dims_in, 256), nn.ReLU(),
nn.Linear(256, dims_out))
perm = Ff.Node(in1, Fm.PermuteRandom, {}, name='Permutation')
split1 = Ff.Node(perm, Fm.Split, {}, name='Split 1')
split2 = Ff.Node(split1.out1, Fm.Split, {}, name='Split 2')
actnorm = Ff.Node(split2.out1, Fm.ActNorm, {}, name='ActNorm')
concat1 = Ff.Node([actnorm.out0, in2.out0], Fm.Concat, {}, name='Concat 1')
affine = Ff.Node(concat1, Fm.AffineCouplingOneSided, {'subnet_constructor': subnet},
conditions=cond, name='Affine Coupling')
concat2 = Ff.Node([split2.out0, affine.out0], Fm.Concat, {}, name='Concat 2')
output1 = Ff.OutputNode(split1.out0, name='Output 1')
output2 = Ff.OutputNode(concat2, name='Output 2')
example_INN = Ff.GraphINN([in1, in2, cond,
perm, split1, split2,
actnorm, concat1, affine, concat2,
output1, output2])
# dummy inputs:
x1, x2, c = torch.randn(1, 100), torch.randn(1, 20), torch.randn(1, 42)
# compute the outputs
(z1, z2), log_jac_det = example_INN([x1, x2], c=c)
# invert the network and check if we get the original inputs back:
(x1_inv, x2_inv), log_jac_det_inv = example_INN([z1, z2], c=c, rev=True)
assert (torch.max(torch.abs(x1_inv - x1)) < 1e-5
and torch.max(torch.abs(x2_inv - x2)) < 1e-5)