About
On this site we want to present our work on the energy minimization of graphical models that is also known by various other names (e.g. MAP-inference, Weighted Constraint Satisfaction, etc.).
The optimization task is NP-hard in general and can be expressed by the following formula
\[ \min_{x\in\mathcal X_{\mathcal V}} \left[ E_{\mathcal G}(\theta,x) := \sum_{u\in\mathcal V} \theta_u(x_u) + \sum_{uv\in\mathcal E} \theta_{uv}(x_u, x_v) \right]. \]
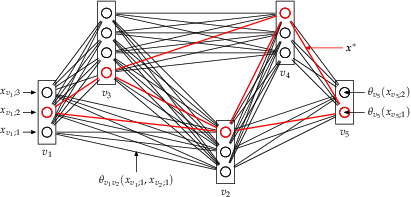
The CombiLP-algorithm considers relaxations where the original problem is decomposed into two non-overlapping parts: an easy LP-tight part and a difficult one. For the latter part a combinatorial solver must be used. As shown in experiments, in a number of applications the second, difficult part constitutes only a small fraction of the whole problem. This property allows to significantly reduce the computational time of the combinatorial solver and therefore solve problems which were out of reach before.
References
- B. Savchynskyy, J. Kappes, P. Swoboda, C. Schnörr.
Global MAP-Optimality by Shrinking the Combinatorial Search Area with Convex Relaxation.
NIPS-2013. [pdf] - S. Haller, P. Swoboda and B. Savchynskyy.
Exact MAP-Inference by Confining Combinatorial Search with LP Relaxation.
Accepted to AAAI 2018. [pdf]
Examples and Experiments
In these illustrations for common benchmark problems the final ILP subproblem is highlighted in red. Only this red part is touched by the ILP solver and the solution for the other areas is purely inferred by an LP solver. As the (approximate) LP solver that are used in practice are converging extremely fast and an ILP solver is orders of magnitudes slower, by reducing the size of the ILP subproblems we can achieve massive speed-ups.

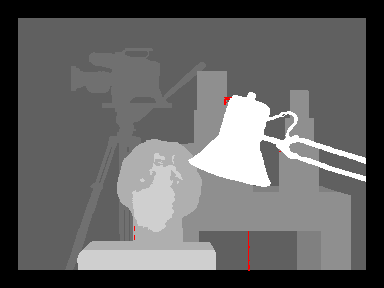





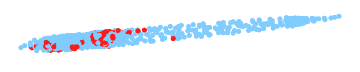
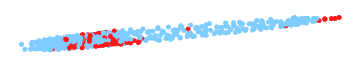


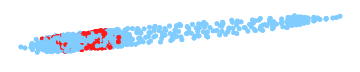




More experiments are available on a seperate page.
Source Code
Our repository contains a re-implementation of the CombiLP algorithm in Python. The original implementation was done by Bogdan Savchynskyy and has been integrated into opengm. I rewrote the whole C++ code base to clean everything up and implemented some major improvements (see references above).
Before working on this port to Python I added functionality to the opengm code myself. Unfortunately, this tight integration into opengm came with a price and during development quick tests almost always resulted in a huge amount of boilerplate code. At some point I started working on a complete independent re-implementation. Note that performance is not a goal and this is all about simplicity and maintainability. It should be behave more or less like the C++ implementation, though (see “Was has changed?”).
IMPORTANT: Note that this is the not the code used for the latest paper, but it should be comparable and much easier to use and hack on, see next section.
What has changed?
Compared to the original implementation many things have changed. The whole logic has be completely rewritten in Python. The subsolvers (that perform the “real” work) are still C/C++ libraries so their performance is not affected. The overall pipeline has not changed much, so all the critical characteristics (number of CombiLP-iterations, sizes of the ILP subproblems, etc.) are more or less identical as in the original implementation.
As the reparametrization is currently implemented in Python it is much much slower than before. It would be quite easy to accelerate everything using Cython or similar techniques. If you look at the summary of the elapsed running time, chances are very high that you are only interested in the time actually spent computing ILP solutions.
I do not have any plans to speed up the reparametrization right now, as in a serious implementation this time would be almost zero and the real speed-ups come from the reduced size of the ILP suproblem.